Mathematik

Einleitung
Im Referendariat habe ich einige Stunden und Reihen gründlich geplant, die ich hiermit anderen Referendaren, Lehrern oder andersweitig Interessierten erstmal als Orientierung zur Verfügung stellen möchte. Die einzelnen Aufgaben und Lösungen werde ich demnächst ebenfalls als Materialpool ins Netz stellen. Trotz der gewissenhaften Ausarbeitung übernehme ich keine Gewähr für die Richtigkeit der Angaben.
Verlaufsschema: Kurvendiskussion
Vorgehensweise
Gegeben ist eine Funktion f (x) in einem Definitionsbereich D(f) = [ a , b ]
Schnittpunkte mit y-Achse
f (0) = y mit Sy ( 0 / y )
Schnittpunkt mit der x-Achse
f (x) = 0 (Horner-Schema)mit Sx1 ( x1 / 0), Sx2 ( x2 / 0), usw.
Hinweis: Ein Polynom vom Grad n kann höchstens n Nullstellen haben!
Untersuchung der Extremstellen
Bilden der ersten Ableitung f ´(x)
Notwendige Bedingung
Nullstellen der Ableitungsfunktion berechnen: f ´ (xE) = 0
Erhalte Werte xE1, xE2 usw.
Hinreichende Bedingung
Vorzeichenwechsel von f ´ an den Stelle xE prüfen.
Bei einem Vorzeichenwechsel von f ´ (x) von (+) nach (-)
ist an der Stelle xE ein relatives Maximum: H ( xE / yE )
Bei einem Vorzeichenwechsel von f ´ (x) von (-) nach (+)
ist an der Stelle xE ein relatives Minimum: T ( xE / yE )
Ist kein Vorzeichenwechsel festzustellen, ist an der Stelle xE keine Extremstelle.
oder
Bilden der zweiten Ableitung f ´´ (x)
Einsetzen der möglichen Extremstellen xE in f ´´ (x).
Ist f ´´ (xE) < 0, so ist an der Stelle xE ein relatives Maximum: H ( xE / yE )
Ist f ´´ (xE) > 0, so ist an der Stelle xE ein relatives Minimum: T ( xE / yE )
Ist f ´´ (xE) = 0, so ist an der Stelle xE keine Extremstelle.
Untersuchung der Wendestellen
Bilden der zweiten Ableitung f ´´ (x)
Notwendige Bedingung
Nullstellen der Ableitungsfunktion berechnen: f ´´ (xW) = 0
Hinreichende Bedingung
Bilden der dritten Ableitung f ´´´ (x)
Einsetzen der möglichen Wendestelle xW in f ´´´ (x).
Ist f ´´´ (xW) > 0, so ist an der Stelle xW eine Wendestelle von rechts nach links.
Ist f ´´´ (xW) < 0, so ist an der Stelle xW eine Wendestelle von links nach rechts.
Ist f ´´´ (xW) = 0, so ist an der Stelle xW kein Wendestelle.
Hinweis: Falls der Wendepunkt eine waagerechte Tangente hat (f ´(x) = 0), ist es ein Sattelpunkt.
Graph
Bekannte Stellen (Sy, Sx, T, H, usw.) in Koordinatenkreuz einzeichnen, wobei der Definitionsbereich D(f) = [ a , b ] zu beachten ist.
Kurvenverlauf klar machen und notfalls eine Wertetabelle anlegen.
Zins- und Kapitalrechnung
Kapitalaufbau
| Nachschüssiger Einzahlung |
Vorschüssiger Einzahlung |
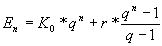 |
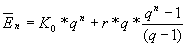 |
Kapitalabbau
| Nachschüssiger Einzahlung |
Vorschüssiger Einzahlung |
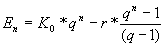 |
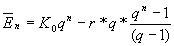 |
Aufgabe 1:
Ein Kaufmann verfügt am Anfang eines Jahres aus einer Erbschaft über einen Betrag von 30.000,00 DM. Er legt das Geld zu 5 % Zinsen an. Wieviel Jahre lang kann er jährlich vorschüssig 3.700,00 DM aus dem Guthaben entnehmen, bis das Kapital vollständig aufgebraucht ist.
Aufgabe 2:
Ein Sparkonto weist am Anfang eines Jahres einen Bestand von 13.800,00 DM auf. Der Sparer zahlt jeweils am Ende des Jahres 6 Jahre lang jeweils 1.200,00 DM auf das Sparkonto ein. Über welches Guthaben verfügt der Sparer am Ende des 6. Jahres, falls 4,5 % Zinsen von der Bank gewährt werden.

